Can you solve this maze?
Is it too easy?

How about this one?
Still doable right?

What about this one?
Doesn't it break your will to solve just by looking at its size right?

I will tell you a little secret on how to solve any maze with ease!
We can think of the three mazes above as topologically identical mazes.
If you approach them topologically, you will be able to solve any maze with very little effot if you have little bit of painting skills.

In topology, heomeomorphism is defined as

...No need to read/undertsand that :D

Simply put, two objects are called heomeomorphism when one object can be deformed(stretching, shrinking, bending) to look like other obejct. Imagine I have a clay cup, I can strech, shrink, and bend to make a donut shaped clay. This is all you need to understand to solve maze using topology.

Let look at the first maze again.

This maze consists of two straight lines.
I will color top line with orange, and bottom line with blue.

What would be the solution of this maze?

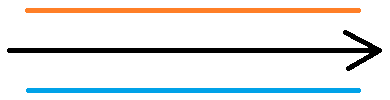
It will simply be crossing between the orange line and blue line right?
Lets bring the second maze.

This maze is actually heomeomorphic with the first maze.
What does that mean?

If you color the line on the left with orange and line on the right with blue, the maze is divided into exactly two lines.
Huh, maze with just two lines? Sounds familiar...
If I remember correctly, I could just solve a maze with two lines by simply crossing between the two lines.
Let's try that for the second maze.

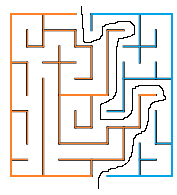
Wow, that was easy.
Let's look at our final maze.

Again, I will color left line with orange and right line with blue.

Now, if I draw a line that crosses between the two colors,

You can solve this maze with ease.
There could be some case where a maze consists of multiple lines, but will not affect heomeomorphism of a maze.

With Holiday season coming up, impress your maze solving buddy with this mind-blowing method!